논문을 상세히 번역하고 한단어씩 해석해주는 포스팅은 많다.
나는 논문을 누구나 알아듣도록 쉽고 간결하게 전달하고자 한다.
GCN
저자의 의도
그래프 구조 데이터에 대한 semi-supervised learning 방법을 제안한다.
기존 spectral graph method의 속도 문제를 localized convolution으로 개선한다.
기존 spectral graph method는 시간 복잡도가 O(n³) 이다.
저자들의 방법을 사용하면 선형 시간 복잡도 (O(n))를 가질 수 있다.
로컬 그래프 구조와 노드의 특징을 모두 인코딩할 수 있다.
기존 문제점
1. 용량 문제
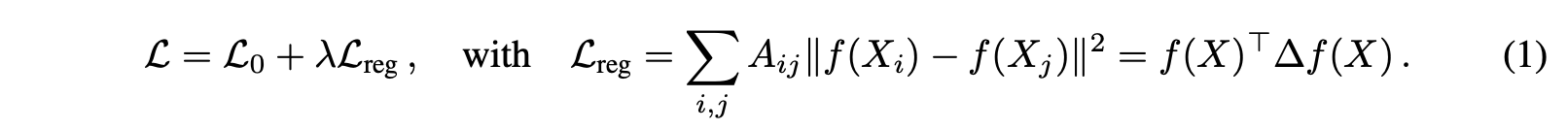
와! 복잡한 수식이다. (쉽게 설명한다며! ㅇㅅㅇ)
걱정 말자 쫄지말고 천천히 따라가면 별로 안어렵다.
[변수 설명] (안 읽어도 됨)
L: 기존 loss function, 지도학습 목적
L_0: 지도학습 loss, 레이블이 있는 노드에 대한 loss
L_reg: 그래프 정규화 loss, 연결된 노드들이 유사한 특징을 갖도록 하는 텀
f 함수: 인공신경망을 의미하는 미분 함수
X: node feature matrix, 노드의 특징 행렬
∆: normalized 되지 않은 라플라시안 행렬, (= D - A)
A: adjacency matrix, 노드간 연결 정보, 0 or 1로 구성
D: degree matrix, 노드의 차수 정보, 연결된 엣지 수가 대각 원소
기존 loss function은 다음 가정을 바탕으로 만들어졌다.
가정: 연결된 노드끼리 동일한 레이블을 공유할 가능성이 높다.
그러나 이 가정 때문에 모델은 과도한 계산 비용을 사용해야 한다.
왜냐하면 라플라시안 행렬 ∆는 그래프의 모든 노드 간의 관계를 포함하고 있는데,
그래프 크기가 커질수록 ∆의 크기도 기하급수적으로 커진다.
∆는 노드 간의 관계에 대한 행렬이므로 노드 개수의 제곱에 비례하기 때문이다.
따라서 ∆를 계산하기 위해 과도한 계산 비용이 필요하다.
(실제 쇼핑 같은데 적용하려니 노드가 너무 많다. 노드는 유저와 상품을 말한다.)
하지만 저자들은 그래프의 모든 노드 간의 관계를 고려할 필요가 없다고 주장한다.
localized convolution을 통해 로컬 구조만 고려하려는 것이다.
그리고 localized convolution이 해당 논문의 주된 내용이다.
2. 간접 인코딩
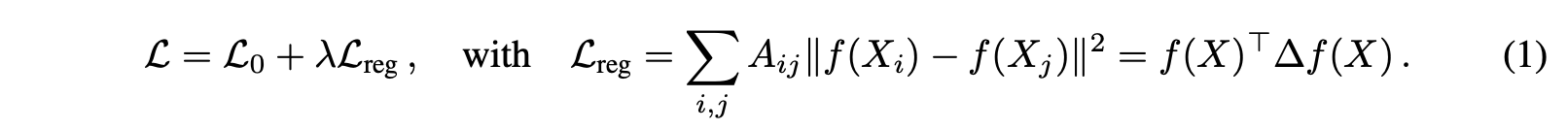
기존 loss function은 A 행렬에 대하여 암묵적으로 그래프 기반 정규화를 진행한다.
Eq1을 봤을 때 A행렬에 대하여 직접적으로 f를 적용하지 않고 f(X)를 활용한다.
라플라시안 행렬 ∆ (= D - A)를 통해 간접적으로만 그래프 구조를 활용한다.
그러나 우리가 알고싶은건 A 행렬이고 A 행렬에 대한 직접적인 인코딩이 필요하다.
저자들이 제안한 방법은 f(X, A)를 사용해 그래프 구조를 직접 인코딩하는 것이다.
f를 A 행렬에 직접 적용하는 것은 큰 장점이 있다.
지도학습 loss L_0의 그라디언트 정보를 레이블이 없는 노드에도 전파시킬 수 있다.
그 이유는 A는 레이블이 없는 노드도 연결되어 있기 때문이다.
기존 방법은 f(X)이므로 레이블 노드에서만 loss를 계산하고 역전파된다.
반면에 f(X, A)를 사용하면 A 행렬을 통해 연결된 모든 노드가 영향을 받는다.
따라서 레이블이 있든 없든 모든 노드의 representation을 학습할 수 있다.
다시 말해 그래프의 모든 노드에 대한 레이블이 없어도 학습할 수 있다.
이것이 논문 제목의 semi-supervised learning에 대한 의미이다.
그리고 그래프 구조에서 인코딩을 하는 것은 GCN의 핵심 아이디어 중 하나이다.
이 인코딩은 `Message Passing`을 통해서 일어난다.
기존 방법들은 이 메시지 패싱을 위해 라플라시안 행렬 ∆을 사용했다.
그러나 GCN은 adjacency matrix A를 직접 사용하여 메시지 패싱을 한다.
해결 아이디어
1. Fast Approximate Convolutions on Graphs
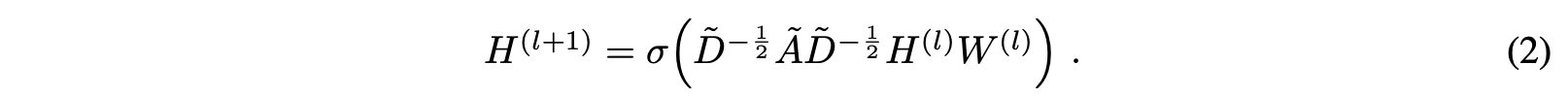
와! 또!!! 복잡한 수식이다. (쉽게 설명한다며! ㅇㅅㅇ)
이 논문이 그림은 없고 수식 뿐이라 어쩔 수 없다...
말은 쉽게 설명할테니 천천히 따라 와보자.
이 섹션에서는 f(X, A)의 이론적 모티브를 소개한다.
저자들은 멀티 레이어의 GCN 아키텍처를 제안했다.
해당 아키텍처의 레이어 별 전파 규칙은 Eq 2와 같다.
[변수 설명] (안 읽어도 됨)
A틸드: A + I_N, adjacency matrix에 자기 자신을 더한 행렬
A: adjacency matrix, 노드간 연결 정보, 0 or 1로 구성
I_N: identity matrix, self connection을 위한 대각 행렬
D틸드: Degree matrix, 노드의 차수 정보, 연결된 엣지 수가 대각 원소
W: weight matrix, 학습 가능한 가중치 행렬
σ: activation function, ReLU 등
H: node feature matrix, 노드의 특징 행렬
2. Spectral Graph Convolutions
저자들은 그래프 구조에 spectral convolution 적용을 제안했다.
여기서 spectral은 행렬의 스펙트럼, 즉 고유값 분해를 의미한다.
선형대수를 배우던 시절을 떠올려보자.
고유값 분해는 행렬을 고유벡터와 고유값으로 분해하는 것이다.
이 고유값 분해 연산 비용은 O(N^2)으로 매우 높은 편이다.
그리고 그래프의 노드 개수가 많아질수록 이 비용은 기하급수적으로 증가한다.
그리고 이 문제를 해결하기 위해 제안된 것이 Chebyshev 다항식이다.
Chebyshev 다항식은 그래프의 스펙트럼을 잘 `근사`할 수 있다.
따라서 고유값 분해를 Chebyshev 다항식으로 대체한다.
Chebyshev 다항식의 연산 비용은 O(|E|)으로 훨씬 낮다.
(그래프 구조에 spectral conv를 하는데 비싼거 말고 싼 Chebyshev를 사용하는 것)
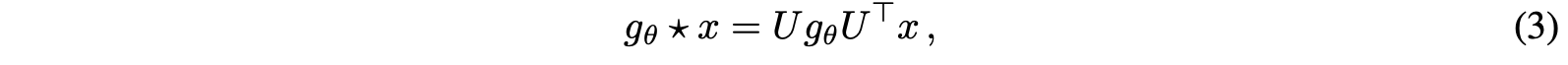
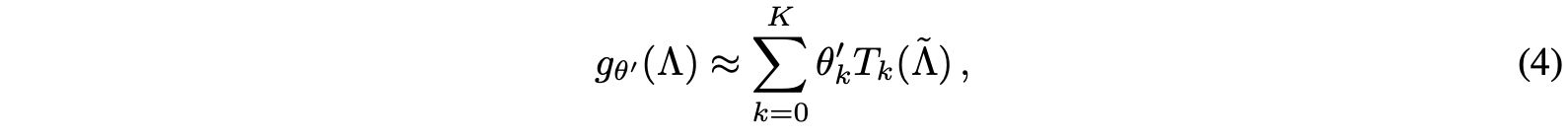
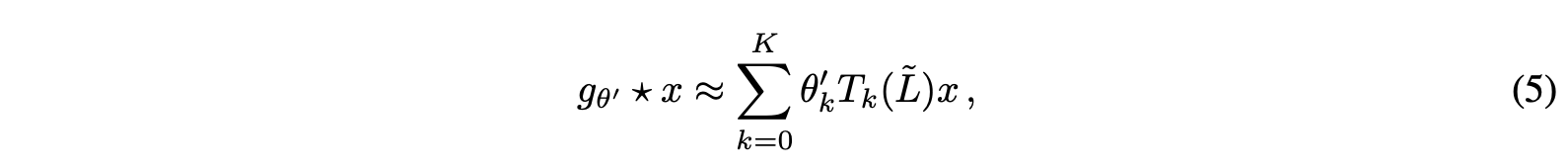
이 과정이 Eq 3 -> Eq 4 -> Eq 5로 변환되는 과정이다.
Eq 5는 GCN의 전신인 ChebNet의 핵심 수식이다.
3. Layer-wise Linear Model
graph convolution 기반의 신경망 모델은 이제 여러 층을 쌓을 수 있다.
이 한층 한층이 Eq 5이 되는 것이며 각각이 비선형성을 가진다.
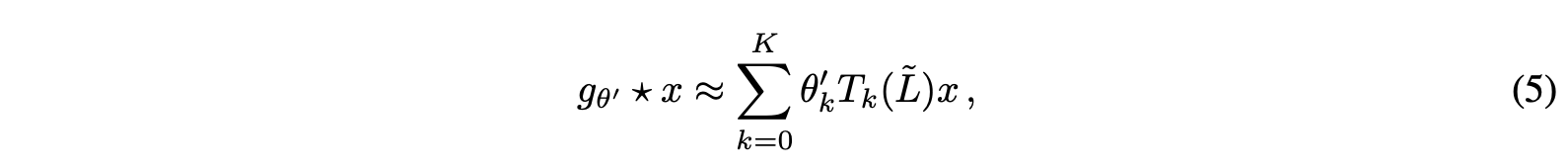
Eq 5에서 K는 필터의 수용 범위를 뜻한다.
K=1일 때는 바로 옆 이웃 노드까지만 정보를 전달한다.
K=2일 때는 바로 옆 이웃 노드와 그 이웃의 이웃 노드까지 정보를 전달한다.
K가 커질수록 더 복잡한 인코딩이 가능해지고 근사치가 점점 잘 맞는다.
하지만 K가 커질수록 과적합, 계산 비용, 노드가 모두 비슷해지는 문제가 있다.
이제 Eq 5를 K=1으로 제한한다고 상상해보자.
K=1으로 제한해도 레이어를 여러번 쌓으면 여전히 풍부한 정보를 인코딩할 수 있다.
(여러 층을 쌓는다면 바로 옆 이웃이 그 옆 이웃의 정보를 받아올 `예정`이기 때문)
또한 SNS나 놀리지 그래프와 같은 도메인에서 과적합 문제를 완화할 수 있다.
추가적으로 계산 비용이 고정되므로 더 많은 레이어를 쌓은 구조를 만들 수 있다.
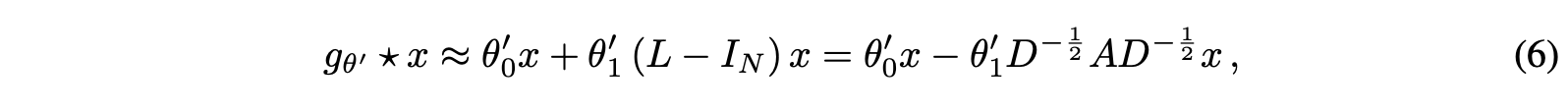
K=1으로 제한할 경우 λ_max=2이며, Eq 5의 식이 단순화되고 Eq 6과 같이 된다.
이제 학습 가능한 파라미터 (free parameters)는 θ_0과 θ_1만 남았다.
이 파라미터들은 다른 말로 filter parameter라고 부른다.
왜냐하면 이 파라미터들은 모든 노드에 동일하게 사용되기 때문이다.
다시 말해 그래프 전체가 공유해서 쓰는 것으로 CNN의 filter와 유사하다.
CNN에서는 이런 필터를 여러번 사용해서 먼 곳의 정보를 받아온다.
(CNN의 receptive field 개념과 ResNet의 혁신적인 이론처럼)
그래프도 마찬가지로 노드에 필터를 여러번 적용해 먼 이웃의 정보를 받을 수 있다.
한번 적용하면 바로 옆 이웃 (1-hop), 두번 적용하면 2-hop 이웃의 정보를 받는다.
이것이 바로 GCN의 핵심 아이디어 중 하나인 Neighborhood Aggregation이다.
Neighborhood Aggregation은 이웃 노드들의 정보를 집계하는 것을 의미한다.
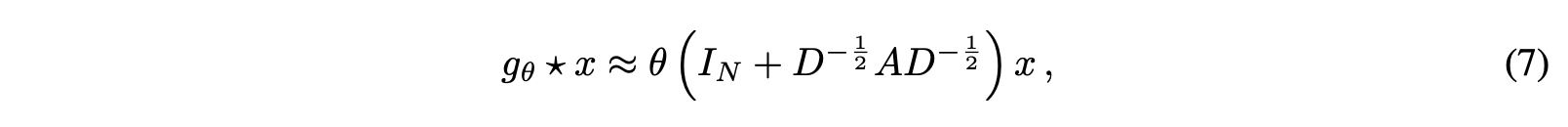
경험적으로 우리가 아는 것은 파라미터 수를 줄이면 두가지 장점을 얻는다.
오버피팅을 방지할 수 있고, 계산 비용을 줄일 수 있다.
따라서 저자들은 θ_0과 θ_1을 하나로 합치는 시도를 했다.
θ = θ_0 + θ_1으로 치환한 식이 바로 Eq 7이다.
이제 식이 매우 간단해진 것을 볼 수 있다.
추가적으로 괄호 안에 있는 텀들은 고유값 범위인 [0, 2]에 속한다.
이 연산을 사용하는 경우에 수치 불안정성이 발생할 수 있다.
또한 뉴럴넷의 고질적인 문제인 exploding/vanishing gradient도 발생한다.
왜냐하면 여러번 곱할 때 1이 넘거나 0이면 발산하거나 사라지기 때문이다.
범위가 [0, 2]이므로 1을 넘는 경우와 0에 가까운 경우가 발생할 수 있다.
이런 문제를 완화하기 위해서 저자들은 renormalization 트릭을 적용한다.
A틸드: A + I_N, adjacency matrix에 자기 자신을 더한 행렬
이 A틸드를 이용해서 D틸드로된 식을 만들면 범위가 [-1, 1]로 제한된다.
그리고 이걸 적용한 식이 바로 Eq 8 이다.
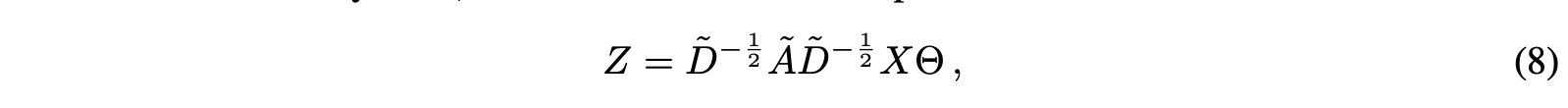
이제 최종 식인 Eq 8이 완성되었다.
[변수 설명] (여긴 읽어 보는 것을 권장함)
X: signal matrix, 입력 행렬
θ: filter parameter, 학습 가능한 파라미터
Z: convoluted signal matrix, 컨볼루션된 출력 행렬
F: filter, 필터, 피처맵
C: input channels, 입력 채널 수
|E|: edge count, 그래프의 엣지 수
이 연산의 연산 비용은 O(|E|FC)으로 기존 O(N^2)에서 크게 개선되었다.
일반적으로 |E|는 N^2보다 훨씬 작다.
4. Semi-supervised Node Classification
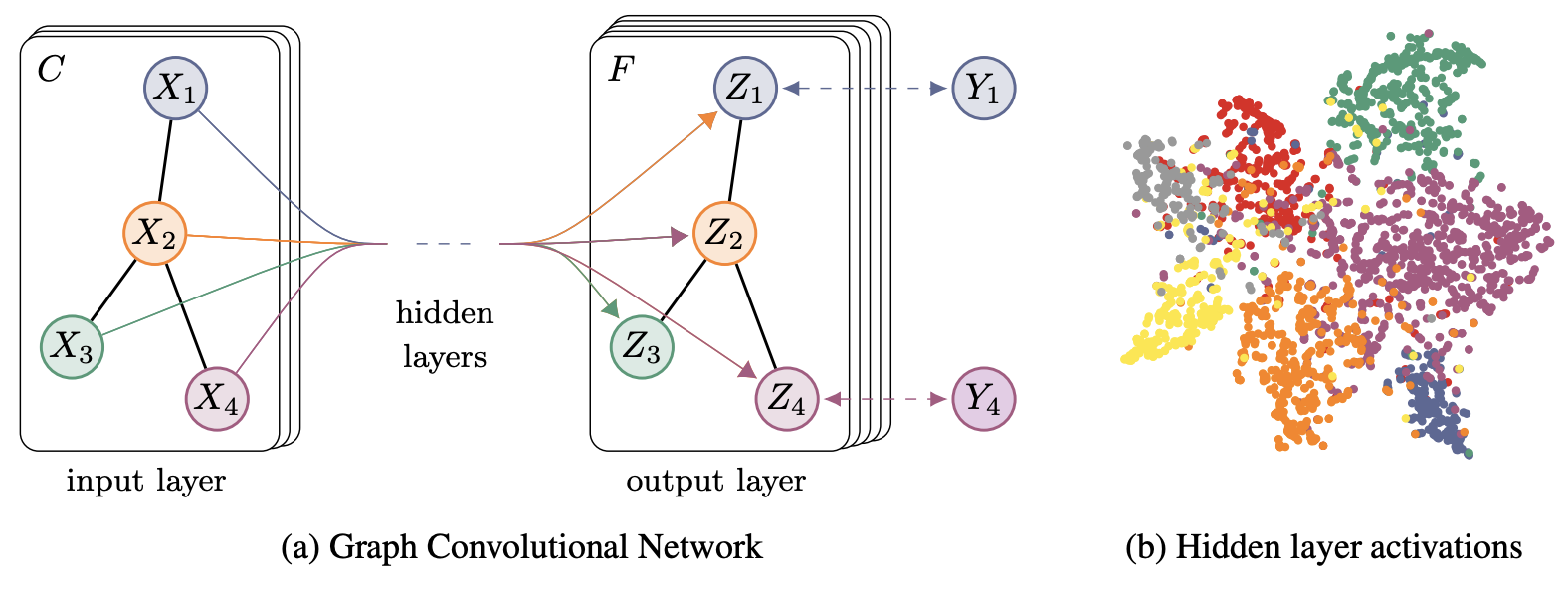
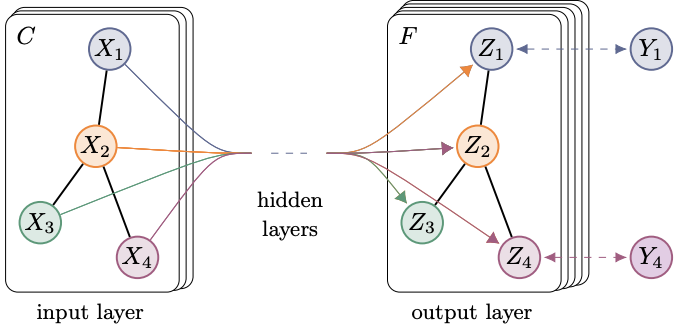
와! 드디어 그림이다!
그래프 구조에서 정보전달을 간단하고 유연하게할 수 있는 모델 f(X, A)를 제안한다.
저자들은 이 모델을 semi-supervised node classification으로 취급했다.
semi-supervised node classification의 수식은 Eq 10과 같다.
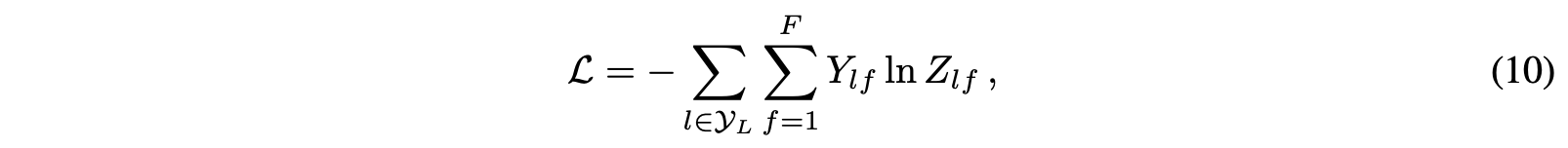
[변수 설명] (안 읽어도 됨)
Y_L: 레이블이 있는 노드들의 인덱스들
Z: softmax, activation function
레이블이 있는 노드들에 대해서만 지도학습 loss를 계산한다.
따라서 일부만 지도학습을 하는 것이므로 semi-supervised 학습이다.
이 연산의 계산 비용은 O(|E|)으로 엣지 수에 비례한다.
결과 분석
1. Datasets
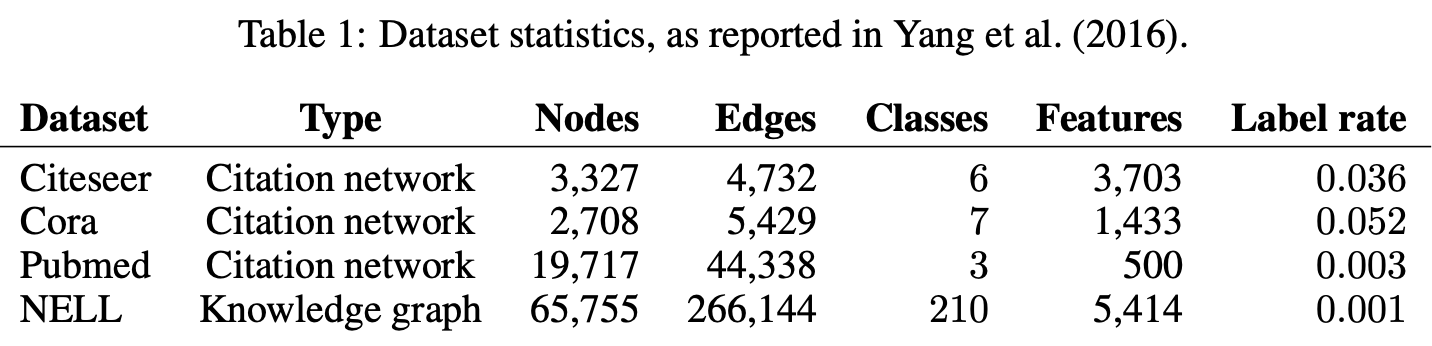
Planetoid 논문의 세팅을 그대로 계승해서 평가했다.
2개의 데이터셋 타입이 존재한다.
Citation network 타입: 노드 = 논문, 엣지 = 인용
Citeseer, Cora, Pubmed
논문은 단어 기반의 feature로 표현되었다. (sparse bag-of-words)
adjacency Matrix A는 인용 관계로 구성했다. (인용 하거나 당하면 1)
각각의 논문은 원래 모두 레이블을 가지고 있다.
(ex. 유전알고리즘 분야, 신경망 분야, 강화학습 분야 등)
학습을 위해 각 레이블당 20개의 논문만 레이블을 붙여 사용했다.
나머지 레이블을 지운 논문들은 특성만 사용했다.
레이블 논문 = 지도학습, 레이블 없는 논문 = 비지도학습
Knowledge graph 타입: 노드 = 엔티티, 엣지 = 연관 관계
NELL
기존의 NELL 데이터셋은 이런 형태이다.
(ex. Paris -(isCapitalOf)-> France, (엔터티 -(연관 관계)-> 엔터티))
기존의 각 관계를 새로운 노드로 바꿔서 (엔티티, 연관 관계) 쌍으로 표현했다.
(ex. (Paris, isCapitalOf), (France, capitalOf))
엔티티는 단어 기반의 feature로 표현되었다. (sparse bag-of-words)
관계의 경우 원 핫 인코딩으로 표현되었다.
그런데 관계가 많아서 이 차원이 61k 정도로 매우 크다.
adjacency Matrix A는 관계가 1개 이상인 경우 1로 설정했다. (binary)
각각의 엔티티는 원래 모두 레이블을 가지고 있다.
(ex. 사람, 도시, 국가, 회사 등)
학습을 위해 레이블당 1개의 엔티티만 레이블을 붙여 사용했다.
나머지 레이블을 지운 엔티티들은 특성만 사용했다.
레이블 엔티티 = 지도학습, 레이블 없는 엔티티 = 비지도학습
2. Experimental Set-up
기본값은 GCN 레이어 2개를 사용한다.
테스트셋의 사이즈는 1000개로 모두 레이블이 있는 샘플이다.
dropout, L2 regularization, early stopping
Adam, epochs=200, learning rate=0.01
3. Results
3.1. Semi-supervised Node Classification
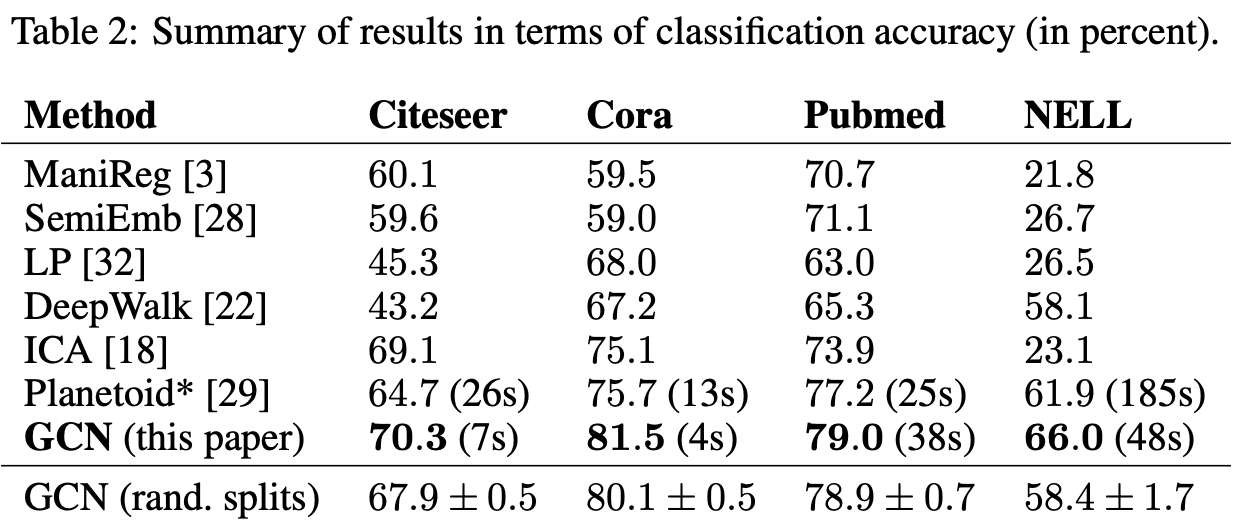
분류 accuracy를 평가 지표로 사용했다.
측정한 accuracy는 100번 시도하여 평균을 냈다.
Planetoid와 GCN의 경우 수렴까지의 걸리는 시간을 함께 표시했다.
기존에 있던 모델들 보다 높은 성능이면서 더 빠른 속도로 추론했다.
또한 기존 모델에 비해 매우 큰 격차로 성능이 좋았다.
그래프 라플라시안 정규화 기반 모델들은 대전제에 의해 한계를 보였다.
(대전제: 엣지는 노드의 유사성을 인코딩한다.)
스킵 그램 기반의 모델들은 최적화가 어려운 다단계 최적화 문제를 가진다.
GCN은 이 두가지 문제를 모두 해결했으며 속도도 가장 빨랐다.
3.2. Evaluation of Propagation Model

저자들은 추가적으로 본인들이 적용한 모든 메서드가 유효한지 검증했다.
최종적으로 완성된 Eq 8에서 하나씩 퇴화시켜가며 Eq 5까지 비교했다.
Eq 5는 ChebNet의 식으로 K가 2일때와 3일때 모두 평가했다.
Eq 6으로 바뀌면서 K=1로 제한된 것인데 성능에 차이가 없으므로 효율적이다.
Eq 7으로 바뀌면서 파라미터수가 감소했지만 성능에 차이가 없으므로 효율적이다.
Eq 8으로 바뀌면서 vanishing gradient 문제를 해결해 성능도 좋아졌다.
3.3. Training Time per Epoch

에포크별 평균 학습 시간을 측정했다.
여기서는 random graphs 데이터셋을 사용했다.
random graphs 데이터셋은 N개의 노드와 2N개의 엣지를 가진 그래프이다.
평가를 위해 만든 임의의 데이터셋이라고 생각하면 된다.
GPU와 CPU-only에서 텐서플로우로 구현해서 실험했다.
엣지가 1k에서 10^-3s 정도의 스케일이고, 1M까지 늘어도 10s 이내로 걸린다.
3.4. Limitations and Future Work
저자들은 GCN이 가진 한계점과 향후 연구 방향을 제시했다.
메모리 문제: 여전히 데이터셋의 크기와 비례하게 메모리 사용량이 증가한다.
특히 GPU 환경에서 10M 엣지의 경우 OOM 에러로 뻗는다. (Fig 2 참고)
엣지 피처 문제: GCN은 엣지 피처를 고려하지 않으며 방향성도 무시한다.
하지만 사실 NELL 평가를 봤을 때 엣지 피처가 필요없을 수 있다.
가정 한계: 지역적인 정보만 받으며, 이웃과 가중치를 동일하게 사용한다.
어떤 데이터셋에서는 셀프 커넥션에 더 높은 가중치를 주는게 좋을 수도 있다.
코드 및 구현
오피셜 코드 없음
GPT와 함께 바이브 코딩
아키텍처
import torch
import torch.nn as nn
import torch.nn.functional as F
# GCN 레이어 구현
class GCNLayer(nn.Module):
def __init__(self, in_features, out_features):
super(GCNLayer, self).__init__()
self.weight = nn.Parameter(torch.randn(in_features, out_features))
def forward(self, X, A):
# A: adjacency matrix (n x n), X: node features (n x in_features)
I = torch.eye(A.size(0)).to(A.device)
A_hat = A + I # A + I (self-loop 추가)
D_hat = torch.diag(torch.sum(A_hat, dim=1)) # degree matrix
D_hat_inv_sqrt = torch.inverse(torch.sqrt(D_hat))
A_norm = D_hat_inv_sqrt @ A_hat @ D_hat_inv_sqrt # 대칭 정규화
return A_norm @ X @ self.weight # GCN 연산
# GCN 모델 정의 (2-layer GCN)
class GCN(nn.Module):
def __init__(self, in_features, hidden_features, out_features):
super(GCN, self).__init__()
self.gcn1 = GCNLayer(in_features, hidden_features)
self.gcn2 = GCNLayer(hidden_features, out_features)
def forward(self, X, A):
x = self.gcn1(X, A)
x = F.relu(x)
x = self.gcn2(x, A)
return x
사용 예시
# 예제: 노드 4개, 피처 3차원, 클래스 2개
X = torch.tensor([
[1.0, 0.0, 3.0],
[0.0, 2.0, 0.0],
[1.0, 1.0, 0.0],
[0.0, 0.0, 1.0],
], dtype=torch.float32)
# 무방향 인접 행렬
A = torch.tensor([
[0, 1, 1, 0],
[1, 0, 1, 1],
[1, 1, 0, 1],
[0, 1, 1, 0],
], dtype=torch.float32)
# 노드 라벨 (예: 2-class classification)
y = torch.tensor([0, 1, 0, 1])
# 학습 가능한 노드 마스크
train_mask = torch.tensor([1, 1, 0, 0], dtype=torch.bool)
# 모델 및 옵티마이저
model = GCN(in_features=3, hidden_features=4, out_features=2)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
loss_fn = nn.CrossEntropyLoss()
# 학습 루프
for epoch in range(100):
model.train()
out = model(X, A) # (n_nodes x n_classes)
loss = loss_fn(out[train_mask], y[train_mask])
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 10 == 0:
pred = out.argmax(dim=1)
acc = (pred[train_mask] == y[train_mask]).float().mean()
print(f"Epoch {epoch}, Loss: {loss.item():.4f}, Train Acc: {acc:.4f}")
'논문리뷰' 카테고리의 다른 글
| [논문 리뷰] DeepFM 요약, 코드, 구현 (0) | 2025.12.18 |
|---|---|
| [논문 리뷰] CLIP 요약, 코드, 구현 (0) | 2025.12.15 |
| [논문 리뷰] LLaMA v1 요약, 코드, 구현 (0) | 2025.03.31 |
| [논문 리뷰] data2vec 요약, 코드, 구현 (3) | 2024.07.16 |
| [논문 리뷰] iBOT 요약, 코드, 구현 (0) | 2024.07.11 |



