딥러닝 모델로 학습을 하면서 가장 많이 겪는 문제점은 hyperparameter 문제다.
learning rate와 epoch를 어떻게 결정하는지가 가장 문제다.
이 문제는 어떤 천재에게 물어도 같은 답이 나온다.
"노가다 말곤 방법이 없어요."
오늘은 그중에서 먼저 learning rate에 대하여 고찰해보자.
일단 간단하게 설명하면 epoch와 batch size를 고정한뒤,
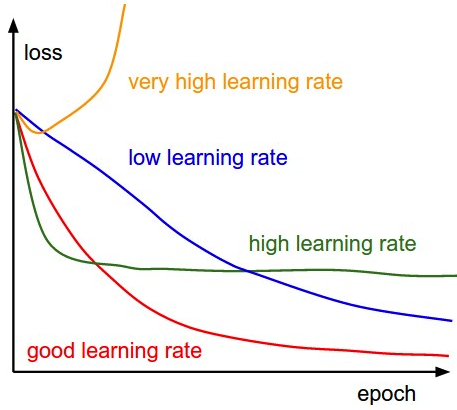
위 그래프를 참고해서 적절한 good learning rate를 찾으면 된다.
그래프를 다 그려가며 비교해보고 좋은 learning rate를 고르자.
즉 learning rate를 x1, x2, x4, x1/2, x1/4 로 학습하며 loss를 그린 뒤에
위 그림을 참고하며 learning rate를 고르면 된다.
CNN이나 작은 데이터셋을 학습할 때에는 이렇게만 하면 된다.
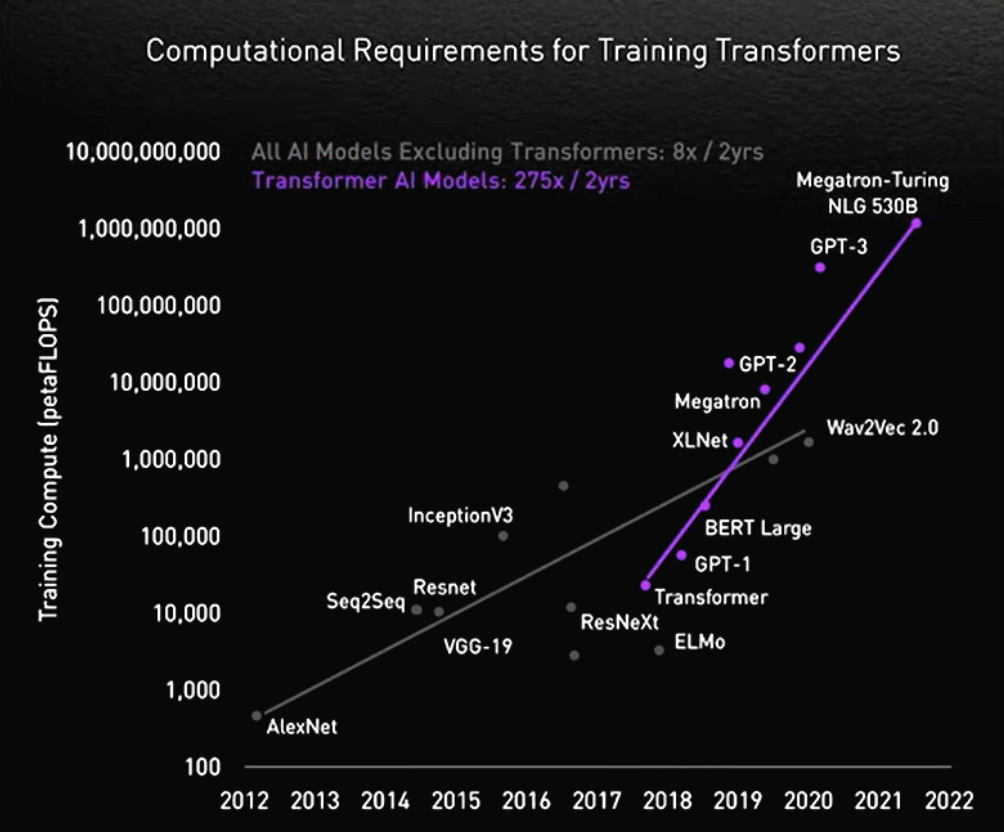
하지만?
언제까지나 CNN만 학습할 수는 없다. 겁나 큰 Transformer가 기다리고 있다....
언제까지나 CIFAR-10이나 학습할 수는 없다. 겁나 큰 ImageNet이 기다리고 있다....
이런걸 학습할 때 문제가 하나 생긴다.
바로 '똥컴 이슈' 이다.
당신이 아무리 맥북을 쓴다고 해도 아무리 개쩌는 데탑을 쓴다고 해도
연구자들이 사용하는 GPU를 따라잡을 수 없다.
구글 클라우드에서 빌려서 코랩으로 돌릴 수 있는 부자라면 괜찮지만,
최소한 나는 아니다 ㅠㅠ....
논문에서 batch size = 1024 와 같이 거대하게 돌렸는데
나는 batch size = 64 와 같이 귀엽게 돌려야 하는 순간이 찾아온다.
이때 우리는 batch size와 learning rate에 관계가 있다는 걸 명심해야 한다.
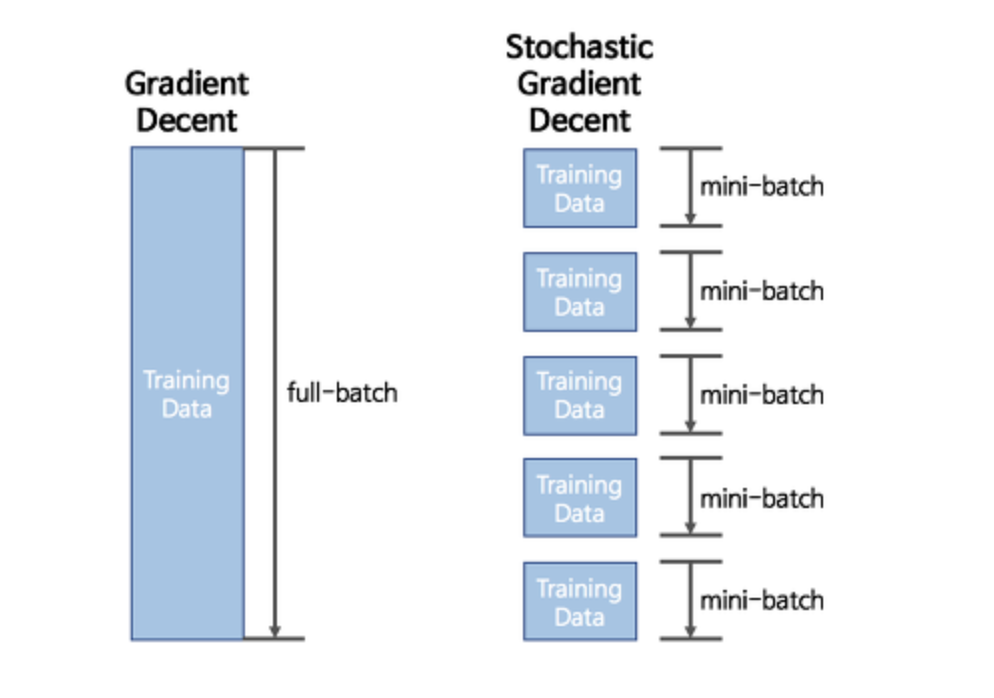
학습 과정에서 loss function으로 해당 mini batch의 loss를 계산해서 그걸 역전파 시킨다.
그말은 batch size가 반으로 줄어들면 learning rate가 2배로 커지는 효과가 난다는 것이다.
왜냐면 배치가 줄어들면 횟수가 2배로 늘어나기 때문이다.
(1개 * (learning rate) = loss) * 1회
-> (1/2개 * (learning rate) = loss) * 2회
그래서 learning rate를 절반으로 줄여주는 것이 필요하다.
정확히는 batch size의 비율 변화를 learning rate에도 동일하게 적용해야 한다.
(예시 : batch size = 1024, lr = 16 -> batch size = 64, lr = 1)
그렇다면 이렇게 보정하고 학습 했을 때 정 확 하 게 동일한 결과가 나올까?
불행하게도 그 답은... '아닐 수도 있다'
이게.......... 상당히 골머리를 썩는 부분이다.
이제 그 이유에 대하여 살펴보자.
여러가지를 설명하면 머리가 복잡하니, 단순하게 장단점만 생각해보자.
다음은 어느정도 보편적인 사실이다. 나를 믿고 따라오자.
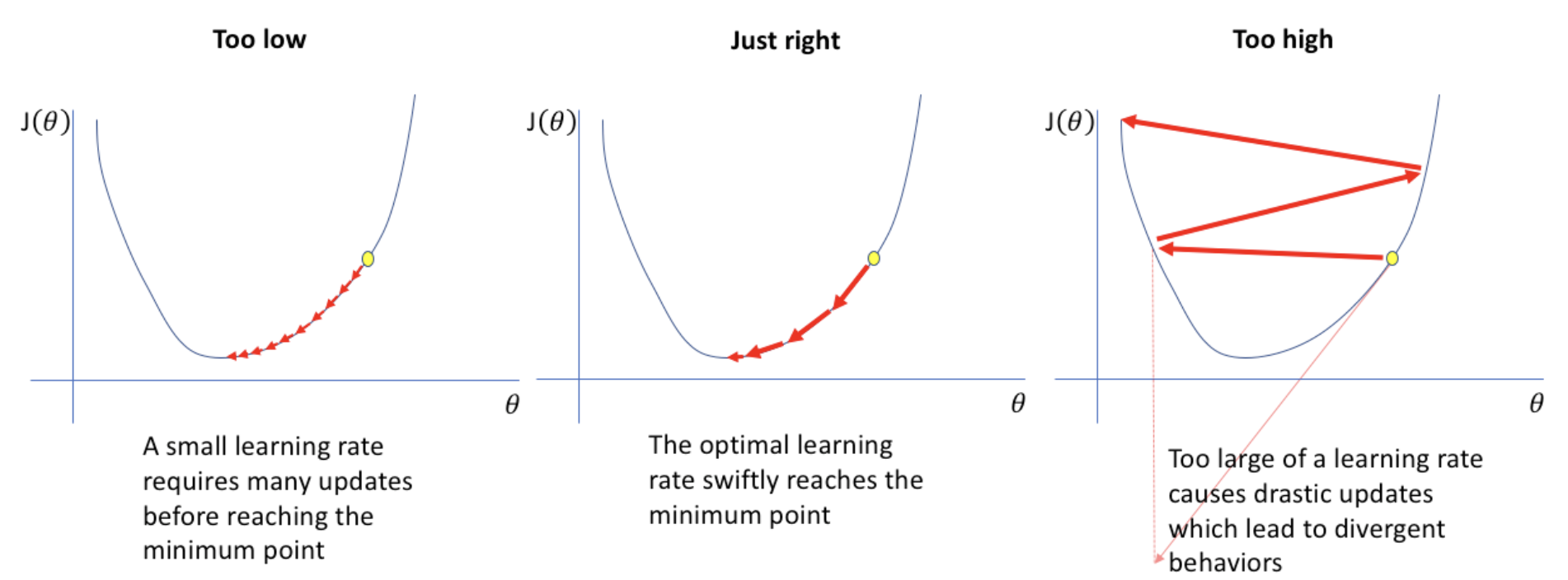
[learning rate]
(high)
장점 : local minimum에 빠질 위험이 적다.
단점 : 너무 빨라 발산할 수 있다.
(+장점 : 빠르다.)
(low)
장점 : 발산하지 않는다.
단점 : local minimum에 빠질 위험이 있다.

[batch size]
(big)
장점 : 더 많은 데이터를 반영하므로 최적값 탐색 경로가 크게 진동하지 않는다. (발산 가능성 X)
단점 : local minimum에 빠질 위험이 있다. (local을 빠져나올 수 있는 특정 데이터 값이 무시된다.)
(+장점 : 더 많은 병렬 연산을 하므로, 빠르고 효율적이다.)
(small)
장점 : local minimum에 빠질 위험이 적다. (local을 빠져나올 수 있는 특정 데이터 값으로 단번에 탈출한다.)
단점 : 적은 데이터를 반영하므로 최적값 탐색 경로가 크게 진동하며 진행된다. (발산 가능성 O)
이렇게 봤을때
high & big 조합은 서로 상충되는 부분 외에도 이점을 더 얻는다.
low & small 조합에 비하여 high & big 조합은 상대적으로 더 빠르고 효율적이다.
그리고 데이터셋의 분산에 따라서 learning rate와 batch size 변화에 민감하게 반응할 수 있다.
그래서 운이 나쁜 경우에는 논문을 정석적으로 환산한 값이 아니라,
case1, accuracy가 미세하게 낮게 나와서 값을 조정하는 번거로움
case2, 과적합 때문에 값을 조정하는 번거로움
두가지 고민을 하게 된다.
ref : (batch size = 1024, lr = 16, epoch = 10)
-> 구현 : (batch size = 64, lr = 1, epoch = 10)
-> case1 : (batch size = 64, lr = 1, epoch = 12) (+early stop)
-> case2 : (batch size = 64, lr = 0.8, epoch = 10)
# case1 에서는 epoch를 늘리는게 리스크가 적다.
# case2 에서는 lr를 줄여야만 더 깊은 optimal minimum을 찾을 수 있다.
이처럼 batch size를 줄이는 그 순간 노가다를 한번 더 해야한다.
100% 똑같지 않으면 해보기 전까지 모르기 때문이다.
epoch를 10% 정도 늘려보고, learning rate를 조금 낮춰보고 비교해야한다.
아니면 운이 좋았길 기도메타도 나쁘지 않다.
끝.
'이론' 카테고리의 다른 글
| [풀스택 딥러닝] 1번째, 딥러닝 개발 인프라와 도구, 파이토치 라이트닝, 허깅페이스, ONNX, 분산 학습 DDP, ZeRO-3, 클라우드 비용, GPU 서버 구축 비용 (0) | 2025.06.16 |
|---|---|
| 딥러닝 공부 순서 정리 (for CV, Computer Vision) (1) | 2025.06.01 |
| FLOPs, #param, throughput 계산, 의미, 관계 (0) | 2024.03.19 |
| 옵티마이저(Optimizer) 설명, 의미, 고찰 - SGD? Adam? (0) | 2023.10.12 |
| 오차 역전파(back propagation) 설명, 의미, 고찰 (0) | 2023.09.18 |



